3. Game Theory

Game Theory

Normal Form Game : for N players if they take actions at the same time.

A normal form game is a tuple $G= (N,A,u)$

• $N$ is a set of $n$ number of players
• $A = A_1 \times \ldots \times A_n$ is an action profile where $A_i$ is the set of actions for playher $i$. Thus, an action profile $a=(a_1,\ldots,a_n)$ describes the sumultaneous moves by all players
• $\mu : A \rightarrow \mathbb{R}^N$ is a rewards function that returns an $N$ -tuple specifying the payoff each player reveives in state $S$. This is called the utility for an action

A pure strategy for an agent is when the agent selects a single action and plays it. If the agent weere to play the game multiple times, they would choose the same action every time.

A mixed strategy is when an agent selects the action to play based on some probability distribution. That is, we choose action $a$ with probabilitu 0.8 and action b with probability 0.2. If the agenty were to play the game an infinite number of times, it would select $a$ 80 % of the time and $b$ 20 % of the time.

A pure strategy can be treat as a mixed strategy: 100 % probability for one action. That is, a pure strategy is a subset of a mixed stragety

weakly dominant and strongly dominant

A strategy is weakly dominant if the utility received by the agent for playing strategy $s_i$ is greater than or equal to the utility received by that agent for playing $s^{'}_{i}$

NASH EQUILIBRIA FOR PRISONER’S DILEMMA

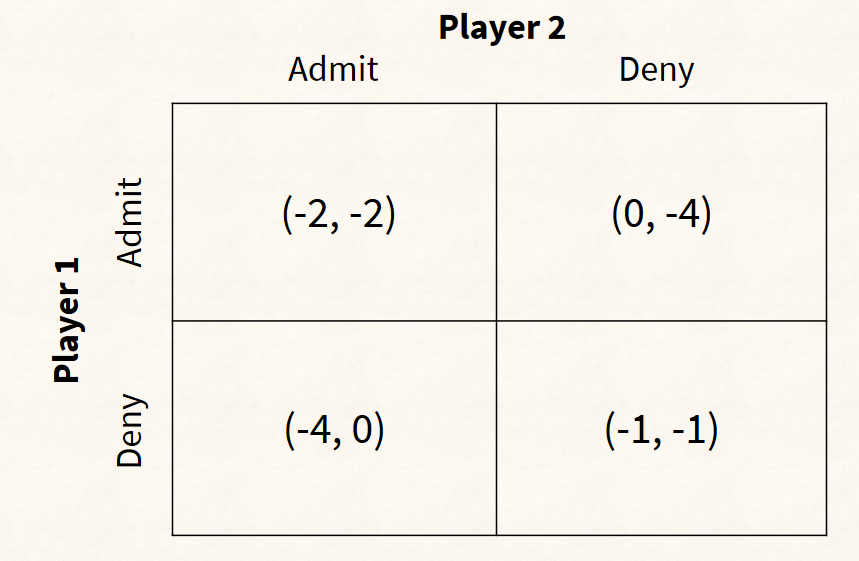
• If player 2 choose Admit, player1 choose admit get greater reward: $-2 > -4$; If player 2 choose Deny, player 1 choose Admit receives greater reward. $0 > -1$
• If player 1 choose Admit, player2 choose admit get greater reward: $-2 > -4$; If player 1 choose Dey, player 2 choose admit get greater reward. $0 > -1$

Nash Equilibrium occurs in a game when each player’s strategy maximizes their own payoff, given the strategies chosen by all other players. No player can gain a higher payoff by unilaterally deviating from their current strategy, assuming the other players maintain their strategies.

Nash's existence theorem

Nash proved that if mixed strategies (where a player chooses probabilities of using various pure strategies) are allowed, then every game with a finite number of players in which each player can choose from finitely many pure strategies has at least one Nash equilibrium, which might be a pure strategy for each player or might be a probability distribution over strategies for each player. reference

Key definations recap:

Interleaved action selection (planning) and action execution is known as online planning.