Skip to main content

FNNs and RNNs

Feedforward Networks

1. Introduction to Feedforward Neural Networks​

  • Feedforward Neural Networks (FNNs): Also called multilayer perceptrons (MLPs).
  • Structure:: Input →\rightarrow Hidden Layers →\rightarrow Output.
  • Neurons:: Each neuron applies weights, adds bias, and passes through a non-linear function (e.g., sigmoid, tanh(hyperbolic sigmoid), ReLU).

2. Mathematical Fromulation​

  • Single Neuron
h=tanh(∑wjxj+b)h = \text{tanh}(\sum{w_j x_j + b})
  • Matrix Notation
h⃗=tanh(Wx⃗+b⃗)\vec{h} = \text{tanh} (W \vec{x} + \vec{b})

3. Output Layer​

  • Binary Classification: Sigmoid activation
  • Multi-class Classification: Softmax activation ensures output probabilities sum to 1.

4. Training and Optimization​

  • Objective: Maximize likelihood L=∏P(yi∣xi)L= \prod P(y_i|x_i), or minimize loss −log⁡L-\log L.
  • Optimizer: Gradient Descent (via frameworks like TensorFlow, Pytorch).
  • Regularization Techniques
    • L1: Sum of absolute values.
    • L2 : Sum of squares.
    • Random Dropout: Randomly zero-out neurons to prevent overfitting.

5. Applications in NLP​

5.1 Topic Classification​

  • Input : Bag-of-words or TF-DF

  • Network:

    • h1=tanh⁡(W1x+b1)h_1 = \tanh(W_1x + b_1)
    • h2=tanh⁡(W2x+b2)h_2 = \tanh(W_2x + b_2)
    • y=softmax(W3h2)y = \text{softmax} (W_3 h_2)

  • Prediction: Class with highest softmax output

5.2 Language Modelling​

  • Goal : Estimate p(w1,w2,wm)p(w_1,w_2,w_m) the probability of word sequences.
  • FFNN LM:
    • Input = embeddings of previous words (e.g., trigram context).
    • Output = next word.
    • Uses learned word embeddings to represent input words.

6. Word Embeddings​

  • Purpose: Map discrete words to continuous vectors.

Recurrent Networks

1. Recurrent Neural Neworks (RNNs)​

Core Concepts​

  • Designed to process sequential data of arbitary length
  • Maintians a State vector to capture information from previous time steps.
  • Process input one token at a time using the Recurrence formula
si=tanh⁡(Wssi−1+Wxxi+b)yi=softmax(Wysi)\begin{align*} &s_i = \tanh(W_s s_{i-1} + W_x x_i + b) \\ &y_i = \text{softmax}(W_y s_i) \end{align*}

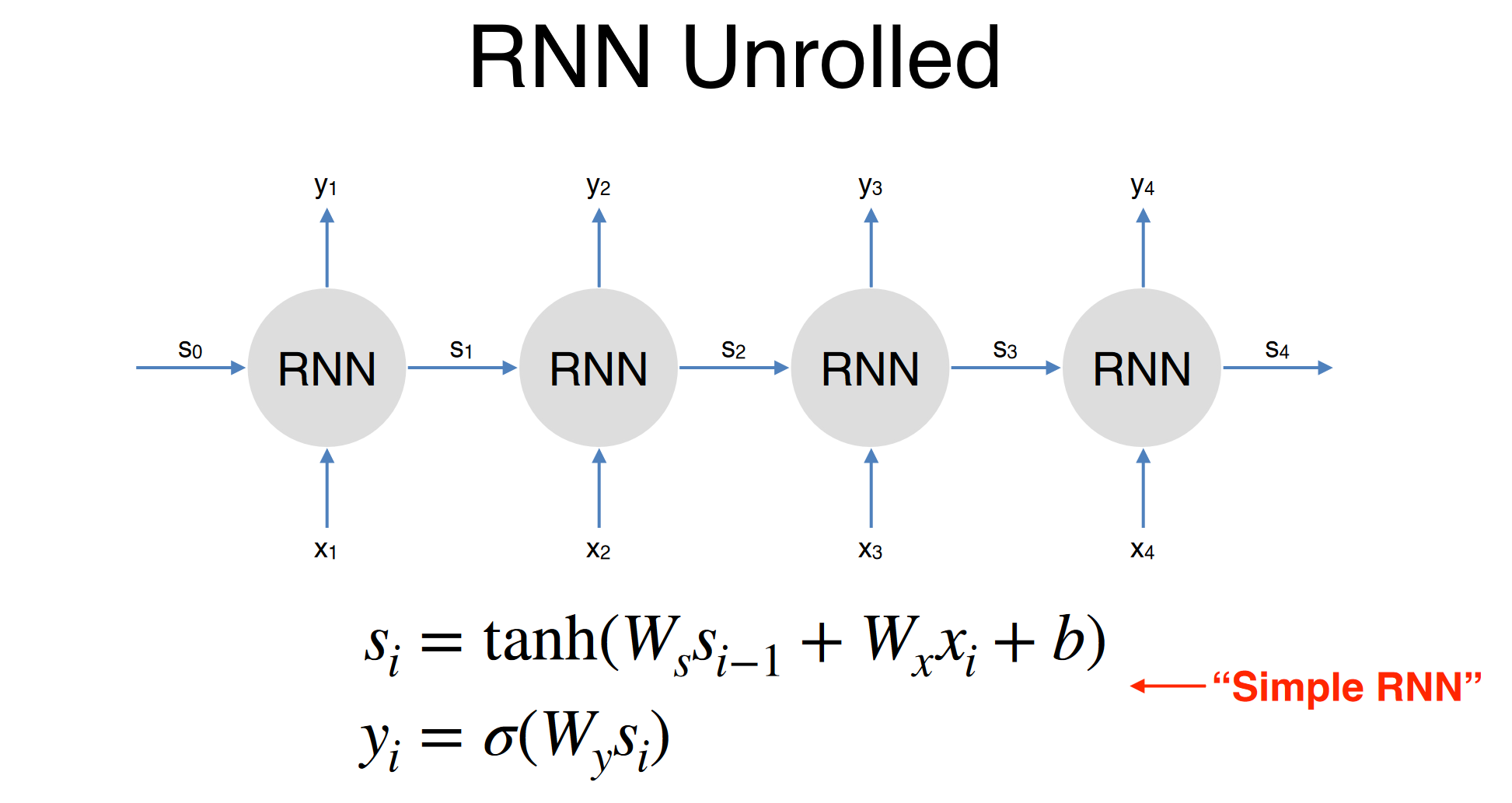
RNN Architecture​

  • Unrolled RNN: each time step reuses the same parameter.
  • Traning uses Backpropagation Through Time(BPTT)
RNN-1

2. Limitaion of RNNs​

  • Difficulty capturing long-range dependencies due to vanishing gradients
  • Performance degrades when trying to model long contexts.

3. Long Short-Term Memory (LSTM)​

3.1 Motivation​

  • Designed to overcome vanishing gradient problems in RNNs.

3.2 Components​

  • Memory cell: stores long-term information
  • Gates: control the flow of information:
ft=σ(Wf[ht−1,xt]+bf)(Forget Gate)it=σ(Wi[ht−1,xt]+bi)(Input Gate)C~t=tanh⁡(WC[ht−1,xt]+bC)(Distilled information)Ct=ft∗Ct−1+it∗C~t(Updated Cell State)ot=σ(Wo[ht−1,xt]+bo)(Output Gate)ht=ot∗tanh⁡(Ct)(Hidden State Output)\begin{align*} f_t &= \sigma(W_f [h_{t-1}, x_t] + b_f) \quad &\text{(Forget Gate)} \\ i_t &= \sigma(W_i [h_{t-1}, x_t] + b_i) \quad &\text{(Input Gate)} \\ \tilde{C}_t &= \tanh(W_C [h_{t-1}, x_t] + b_C) \quad &\text{(Distilled information)} \\ C_t &= f_t \ast C_{t-1} + i_t \ast \tilde{C}_t \quad &\text{(Updated Cell State)} \\ o_t &= \sigma(W_o [h_{t-1}, x_t] + b_o) \quad &\text{(Output Gate)} \\ h_t &= o_t \ast \tanh(C_t) \quad &\text{(Hidden State Output)} \end{align*}
AspectRNNLSTM
Long-term memory❌ Poor✅ Good with gating mechanism
Training speed✅ Faster❌ Slower due to more computation
Expressiveness✅ Flexible✅ Even more expressive
Popularity🔻 Declining🔻 Replaced by Transformers in SOTA