Precepction and Artificial Neural Network

Convolutional Neural Network

Convolution Measures how the shape of one function matches the other as it slides along.

Convolution on 2D images

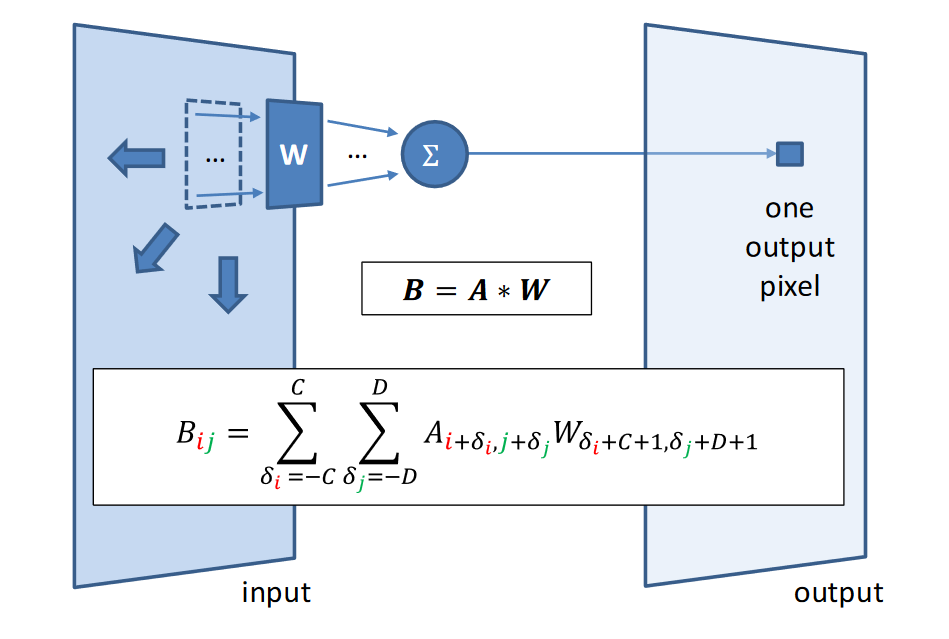
Using filter to perform element-wize multiplication

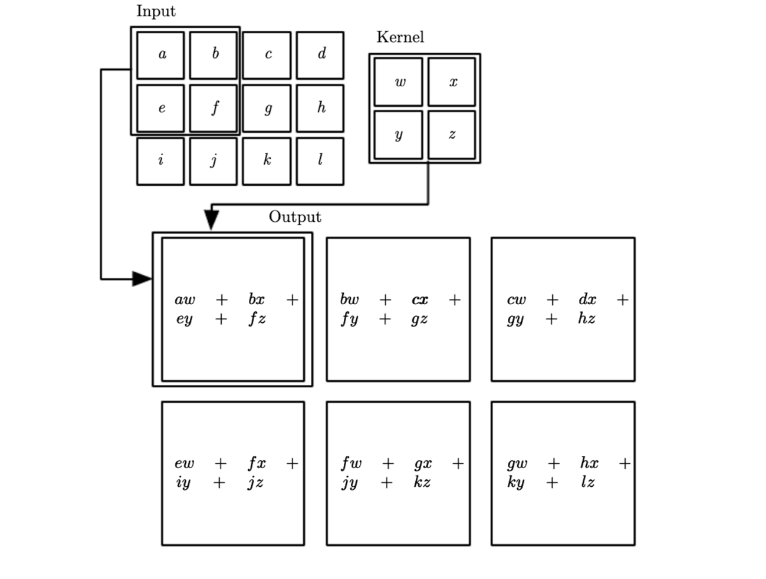
Convolution filters (aka kernels)

Filters/kernels can identify different patterns

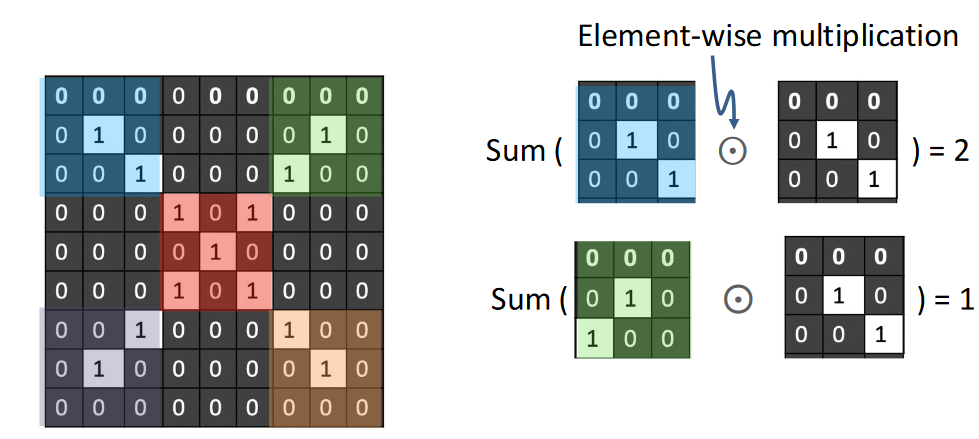
• When input and kernel have the same patern: high activation response

2D example Response map: 2D map of the presence of a pattern at different locations in an input

Convolution parameters

Key hyperparameters in convolution

• Kernel size: size of the patches
• Number of filters: depth(channel) of the input
• Stride: how far to "slide" pacth across input
• Padding of input boundaries with zeros

parameter calculation:

Convolution layer: $\text{k height} \times \text{k width} \times \text{num of inputs} \times \text{num of kernels}$

Output: $\frac{\text{input}- \text{kernel} + \text{padding} \times 2 } {\text{stride}} + 1$

Maxpooling layer: Because the maxpooling extract the feature using functions like $\max$, it does not have parameters

Output: $\frac{\text{input size}- \text{pool size} + \text{padding} \times 2 }{stride} + 1$

Components of a CNN

Convolutional layers

• Complex input representations based on convolution operation
• Filter weights are learned from training data

Downsampling, usually via Max Pooling

• Re-scales to smaller resolution, limits parameter explosion

Fully connected parts and output layer

• Merges representations together

Downsampling via max pooling (re)

Max pooling helps reduce the spatial dimensions (height and width) of the feature maps while keeping the most important information.

• Maxpooling takes an $m \times m$ patch (window) from the input feature map and selects the maximum value from that patch.

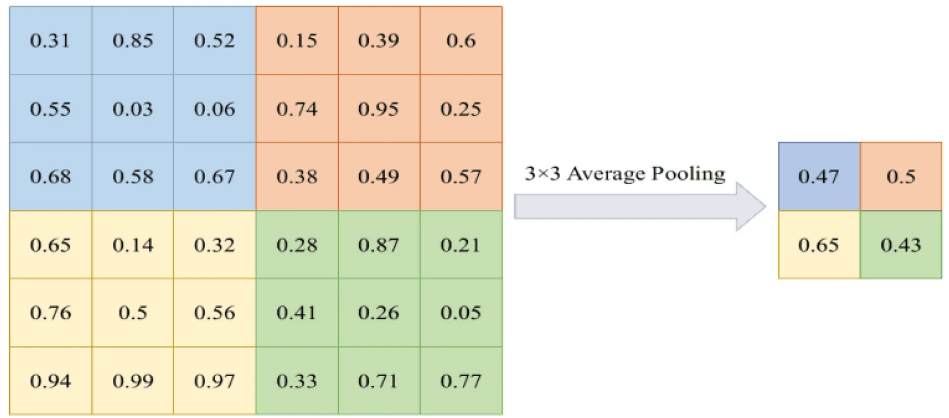
• Forward pass records maximising element, which is then used in the backward pass during back-propagation

Convolution + Max Pooling Achieves Translation Invariance

If the input image is shifted slightly, the network can still recognize the same feature

Consider shift input image:

• exact same kernels will activate, with same responses
• max-pooling over the kernel outputs gives same output
• size of max-pooling patch limits the extent of invariance

Can include padding around input boundaries

Recurrent Neural Networks, Attention, and the Transformer

Recurrent Netwoks

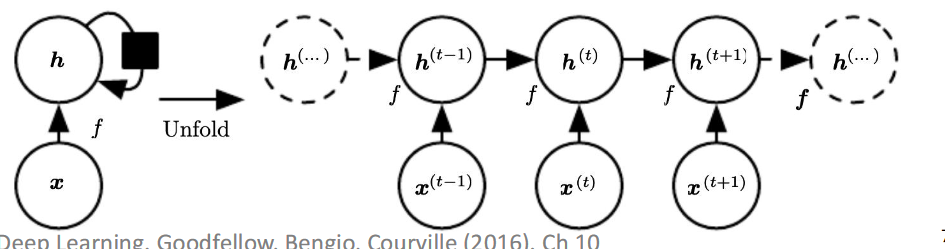
Recurrent Neural Nets(RNNS) RNN creats networks dynamically, based on input sequence.

• Given sequence of inputs $x^{(1)},x^{(2)},\ldots,x^{(t)}$
• Process each symbol from left to right, to form a sequence of hidden state $h^{(t)}$
• Each $h^{(t)}$ encodes all inputs up to $t$

Long Short-Term Memory

• LSTM introduces state self-loop, based on copying
  • Takes copy of previous state, scales by sigmoid forget gate
• Gradient magnitude now maintained
  • Can handle 100+ distance phenimena (vs 5-19 for RNN)

Transformers

RNNs over long sequences not to good at representing proprties of the full sequence

Attention averages over hidden sequence

• Avoids bottleneck, and uncovers meaningful stucture

Self-Atention

• Transformers use attention as means of representing sequences directly, instead of RNN.